Q: Producing through complex processes and using many different kinds of raw and basic materials leads to a lack of accurate calculations on when and how much we are going to need. What happens then is excessive material and insufficient product. Is there a way that we can know precisely the quantity of required material and the time for placing them into the process?
A: I would like to explain the method for calculating material requirements. The diagram below shows the work input and output for one particular process.
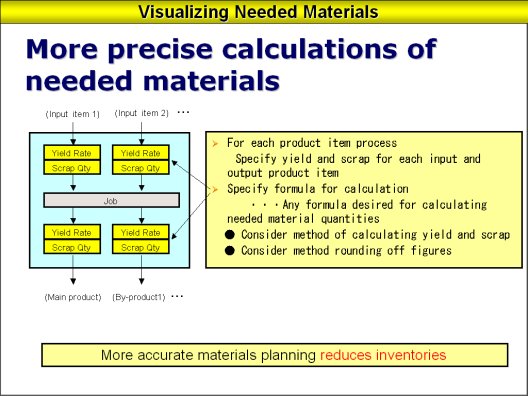
One process has multiple inputs and multiple outputs. When any input item is entered into the process the yield (percentage of good product) for that item will be multiplied and the amount of scrap taken out. That will calculate the volume for the main product. The same goes for the sub product.
With the material requirements we calculate in the opposite direction i.e. we derive the needed quantity for each input item from the quantity of main product. Asprova's calculations for material requirements have functions that allow calculation in either direction. That is to say we can either 1) calculate the volume of product to be produced from the quantity of materials now on hand or 2) calculate the amount of material required from the quantity of product needed. Also because we will have cases in which the material requirement is nonlinear and there is a curve in quantities so we will require functions for calculating that assign the optimum equations.
Calculations of this type can also be used in an MRP (Material Requirement Planning) system. However MRP's fixed lead-time prevents precise calculations of the timing required for materials in theory of constraints scheduling. With theory of constraints scheduling Asprova calculates needed timing and material requirement quantities and trims down inventories of raw materials.
Related articles :
Birth of the Advanced Planning and Scheduling System (APS)
Backward Scheduling for Theory of Constraints (JIT Scheduling)
Forward Scheduling for Theory of Constraints





